再读概率论

在以往我已经在几个不同的领域, 学习了好几次概率论了. 但始终感觉没有把握到概率论的本质, 总是停留在各种概念上. 在这一次, 我再一次学习概率论. 我希望能够寻找一种真正理解概率的方法, 从一个更高的层次理解概率问题. 本文的主要内容来自<<程序员的数学: 概率统计>>, 并结合这本书给出一些自己的理解.

概率的定义

与线性代数一样, 在数学上并不讨论什么是概率, 而是给出了一个概率空间三元组. 只要满足给出的几条性质的东西, 就可以视为概率. 这就相当于在编程中, 只要实现了给定的接口, 就可以直接使用, 而不必关系具体是哪一个类实现.

与线性代数相同，只要满足给定的几个性质的任何东西都可以视为线性代数

概率的上帝视角

由于概率论具有一定的抽象性, 因此引入上帝视角来思考问题. 任意的概率事件, 在上帝视角看来, 都是确定的事件, 只是存在不同的平行世界. 人看起来的概率, 在上帝视角看起来, 实际上是某些世界所占的比例.

上帝视角可以描述成下图的关系.

$$
\begin{matrix}
上帝视角 & \rightarrow & 完全确定的面积问题 & \rightarrow & 面积的答案 \\
—— & & \updownarrow & & \updownarrow \\
人类视角 & \rightarrow & 结果不确定的概率问题 & \rightarrow & 概率的答案
\end{matrix}
$$
从上帝视角看来, 所有的事情都是确定的剧本, 从而消除了所有的不确定性.

所以概率问题实际上就是一个泛化的面积占比问题

三种概率的区别与联系

从连续变量的概率密度函数可以更好的理解联合概率, 边缘概率, 以及条件概率. 例如, 对于一个有两个随机变量的概率密度函数, 其函数图像是三维空间中的一个二维曲面.

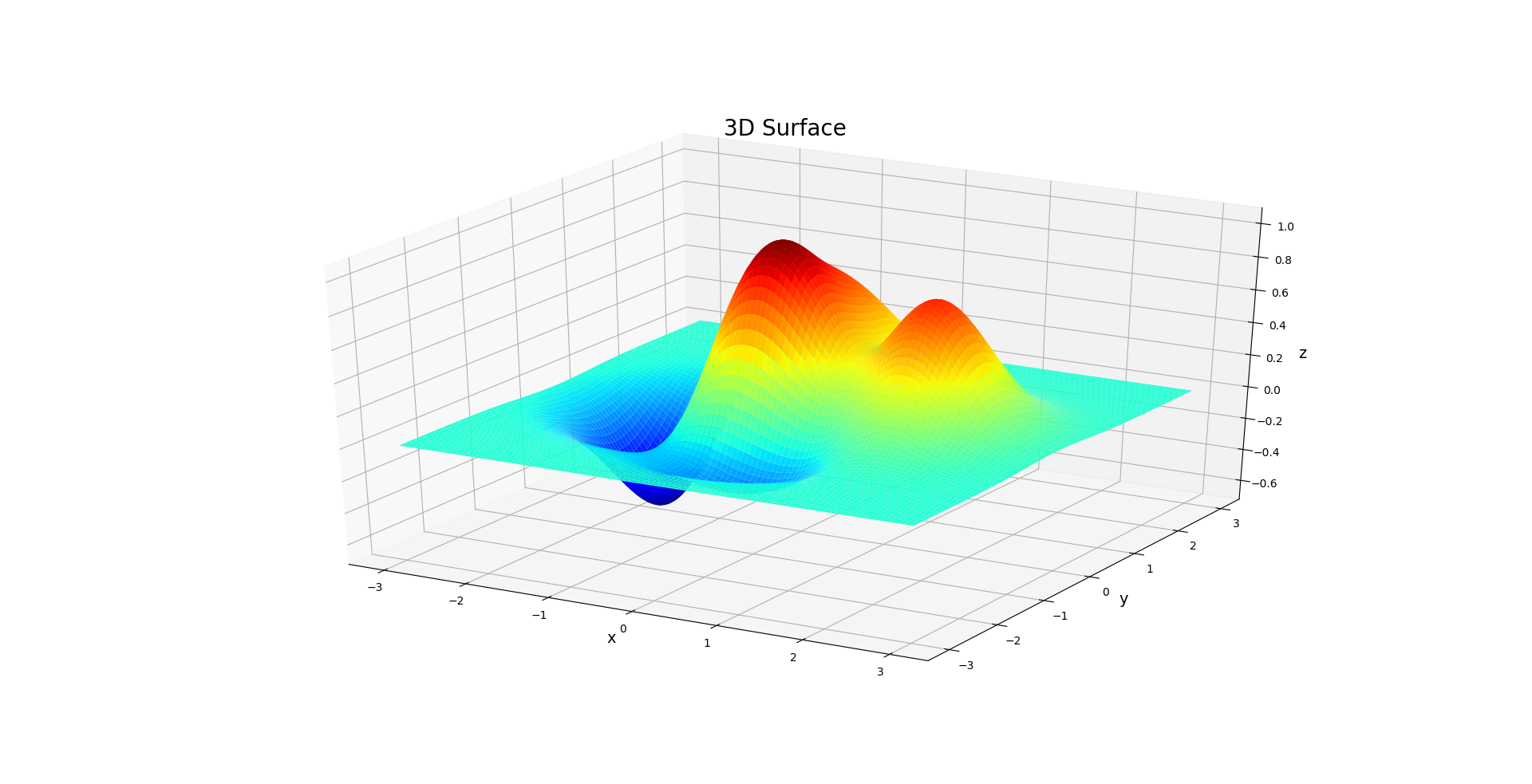
$概率密度曲面$

联合概率实际上就对应了曲面上的一个点, 而边缘概率对应了图像在xOz屏幕和yOz平面上的投影(当然还需要进过积分运算).

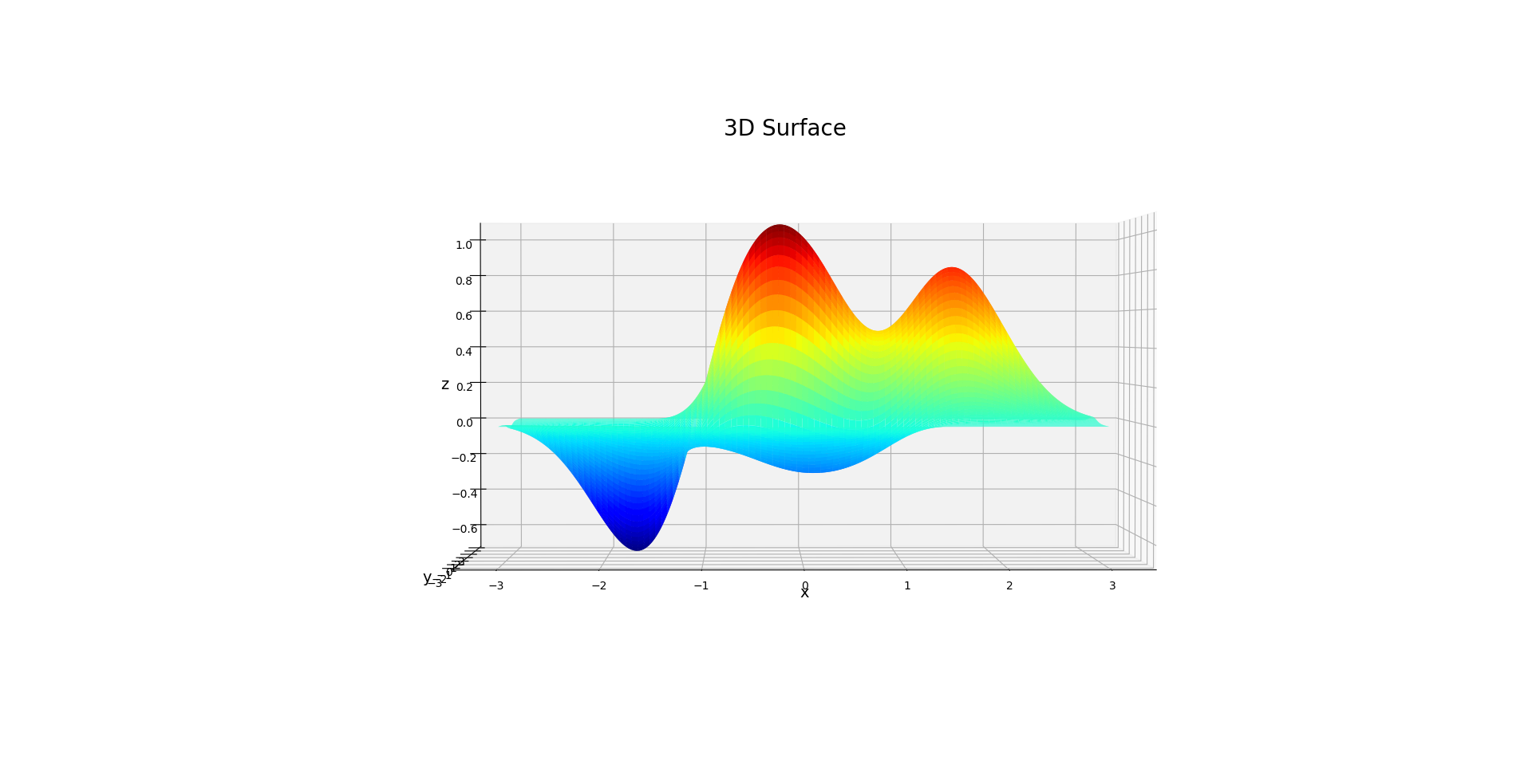
$概率密度曲面X轴方向的投影$

联合概率对应曲面上的一个点, 条件概率对应某一个切面的情况(同样也需要进行处理,才是条件概率的密度函数).

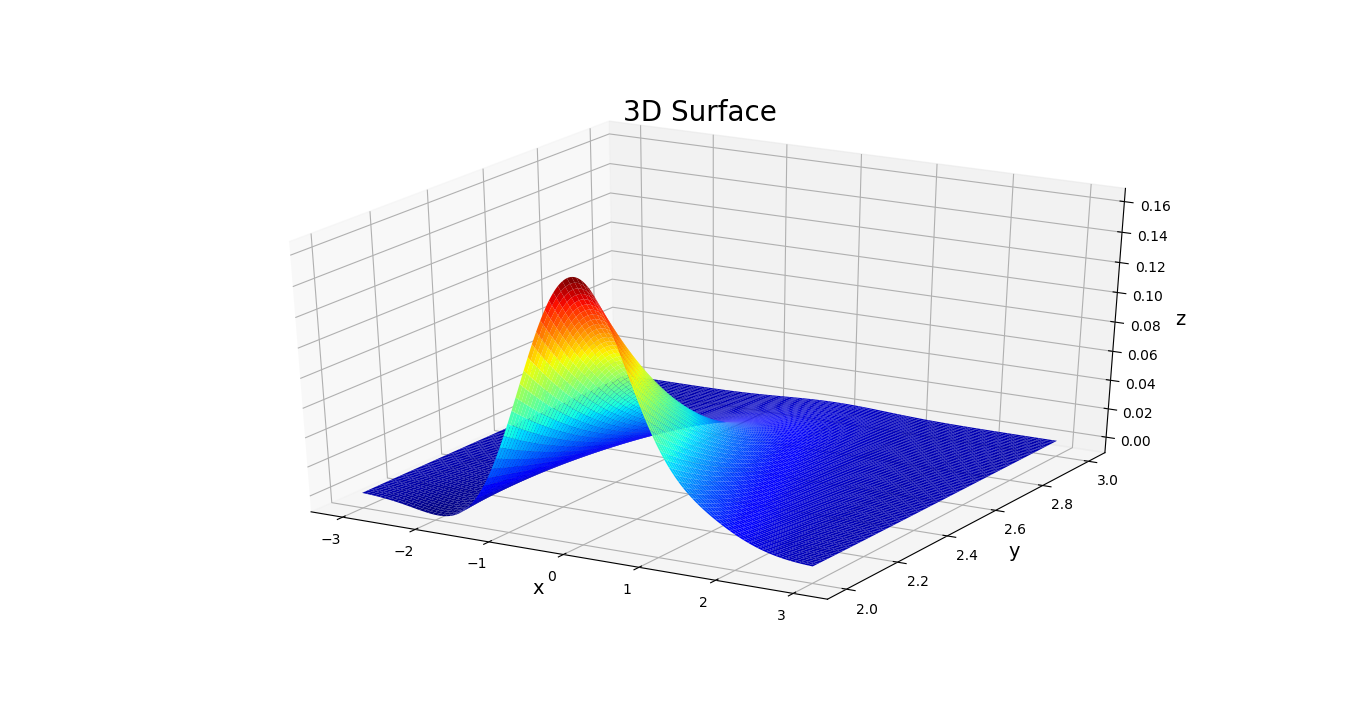
$概率密度曲面切面$

上图为概率密度曲面在Y=2时的切面情况, 这表征了Y=2时,X的分布情况, 也就是条件概率.

独立性

独立性实际上体现的是一种均匀性. 如果随机变量X与Y相互独立, 则说明Y对X的各个值的影响相同, 即对于X的每个具体取值x, Y的各个取值分布相同. 如果是连续变量, 则对于每个具体的x对应的切面, Y的各部分比例都是相同的.

因此独立性不等于互斥, 两个事件互斥, 则不会同时发生, 这显然是不均匀的. 而且不会同时发生也说明了两个之间之间存在某种联系.

贝叶斯公式

贝叶斯公式常用于从结果反推原因的问题. 通常原因X无法被直接观测, 需要通过结果Y来反推. 即已知所有的P(原因)与P(结果|原因), 求P(原因|结果). 如果设原因为A, 结果为B, 则贝叶斯公式可以按照如下的方式推导产生

$$ P(A|B) = \frac{P(A, B)}{P(B)} = \frac{P(B|A)P(A)}{\sum P(B|A_i)P(A_i)}$$

从公式的构成可以发现, 整个公式使用了原因A自身的分布, 以及所有的A->B(原因发生时结果)的概率分布, 求出了B->A(结果发生时原因)的概率分布

期望与方差

对于随机变量X和Y, 有
$$E[X+Y] = E[X] + E[Y]$$

例如, 对于二项分布Bn(n, p), 有
$$E[X] = E[Z1+Z2+…+Zn] = E[Z1]+E[Z2]+…+E[Zn] = p + p + …+ p = np$$

如果随机变量X与Y相互独立, 那么有
$$E[XY] = E[X]E[Y]$$

因为 E[XY] 表示每个位置的X增加Y倍, 如果X与Y相互独立, 则对于每个X而言, Y的分布都是相同的, 因此每个X都扩大Y的平均倍, 即 E[Y] 倍, 因此上式显然成立.

如果X与Y不独立, 则通常不满足上面的等式. 例如统计发现某些人平均每月喝酒8次, 每次平均喝酒1.5瓶, 但每月平均喝酒瓶数为15瓶.

如果随机变量X与Y相互独立, 那么有
$$V[XY] = V[X]+V[Y]$$

将 V[XY] 带入方差表达式, 并展开可知

$$V[XY] = E[(X+Y)-(\mu + \nu)] = V[X]+V[Y]+2E[(X- \mu)(Y - \nu)]$$

由于X与Y独立, 因此等式最后一项值为零.

对随机变量X, 有

$$V[X]=E[X^2]-E[X]^2$$

或者表示为

$$E[X^2]= \mu^2 + \sigma^2$$

大数定理

假设随机变量X1, X2, …, Xn独立同分布, 其平均值定义为

$$Z \equiv \frac{X_1+X_2+…+X_n}{n}$$

于是有

$$E[Z] = E\left [ \frac{X_1+X_2+…+X_n}{n} \right ] = \frac{E[X_1]+E[X_2]+…+E[X_n]}{n} = \frac{n \mu}{n} = \mu$$

由于随机变量X1, X2, …, Xn独立同分布, 因此随机变量和的方差等于各随机变量方差的和, 因此有

$$V[Z] = V\left [ \frac{X_1+X_2+…+X_n}{n} \right ] = \frac{V[X_1]+V[X_2]+…+V[X_n]}{n^2} = \frac{n \sigma^2}{n^2} = \frac{\sigma^2}{n}$$

这说明对同一个事件进行n次重复, 可以使得方差减少到原来的$\frac{1}{n}$, 也即标准差减少到原来的$ \frac{1}{\sqrt{n}}$.

因此如果一项实验希望将误差减少到原来的$\frac{1}{10}$, 则需要进行原来的100倍的实验.

通过以上方差的公式, 我们可以发现, 如果 $ n \rightarrow \infty $, 则 $ V[Z] \rightarrow 0 $ . 方差为零意味着没有随机性, 这说明如果随机变量的数量趋向于无穷, 则他们的平均值将收敛到$ \mu $. 这就是大数定理.

从上帝视角来看, 期望相当于对所有的世界求平均值, 而Z相当于对一个世界的n次重复求平均值. 而大数定理说明这两个平均值在重复次数无限大时会相等. 因此通过大数定理, 在人类视角, 仅观察一个世界的平均值就可以知道全部世界的平均值.

条件期望与条件方差

对于随机变量X和Y, 在X=a时的条件期望是
$$E[Y|X=a] \equiv \sum_{b}P(Y=b|X=a)$$

显然, 当X取值不同的时候, E(Y|X=a)可以取不同的值. 类似地, 也可以定义条件方差, 具体的表达式省略.

中心极限定理

考虑n个独立同分布随机变量X1, X2, …, Xn. 假设这些变量代表各种微小的差异, 为了使其满足误差的含义, 这些随机变量具有以下的特征
$$
\left\{\begin{matrix}
E[X_1]=E[X_2]=…=E[X_n] = 0 \\
V[X_1]=V[X_2]=…=V[X_n] = \sigma^2 > 0
\end{matrix}\right.
$$
如果考虑对上述随机变量和进行标准化操作, 即

$$ W_n = \frac{X_1+X_2+…+X_n}{\sqrt{V[X_1+X_2+…+X_n]}}=\frac{X_1+X_2+…+X_n}{\sqrt{n}\sigma}$$

则$ n \rightarrow \infty $时, $W_n$将趋近于标准正态分布N(0,1). 这说明大量微小的误差叠加后的结果将符合正态分布. 另外, 即使n个独立同分布随机变量X1, X2, …, Xn的期望不等于零, 只要进行标准化操作后, 还是满足上述结论, 即定义
$$W_n = \frac{(X_1-\mu)+(X_2-\mu)+…+(X_n-\mu)}{\sqrt{V[X_1+X_2+…+X_n]}}$$

大数定理和中心极限定理的表达式很接近, 但其中的含义并不相同. 大数定理表明随机变量的和除以n以后收敛于期望值, 而中心极限定理描述了随机变量和的分布情况.

协方差与相关系数

有随机变量X, Y, 其期望分别为$ \mu $, $ \nu $, 则协方差定义为
$$Cov[X,Y] \equiv E\left[(X-\mu)(Y-\nu)\right]$$

可以注意到, 协方差为正数时, 具有以下的特点

一方取值大于期望时, 另一方取值大于期望的概率也更大
一方取值小于期望时, 另一方取值小于期望的概率也更大

同样, 协方差为负数时, 也有相对应的特点. 如果协方差为零, 则不存在这样的相关性.

当X与Y相互独立时, 协方差为零. 因为X与Y独立, 所以Y相对X而言分布均匀, 则对于X大于均值和X小于均值的部分Y放大的倍数相同. 因此最后计算时, X必然在均值上相互抵消, 最后结果为0.

但是反过来, 协方差为零并不能说明X与Y相互独立. 协方差相当于一个评价X与Y线性相关性的指标, X与Y独立时, 必然没有线性相关性. 但没有线性相关性不代表一定没有相关性, 只有存在某种相关关系, 则X与Y就不独立.

对比方差的定义, 协方差显然具有以下的特点

$$Cov[aX+b,cY+d] = acCov[X,Y]$$

由于将随机变量的取值放大, 就可以放大协方差的值, 因此协方差数值的大小无法表现相关性的大小. 针对这一问题, 可以在计算协方差之前, 分别对X和Y进行标准化. 由于期望的偏移不影响协方差的值, 因此可以只进行缩放, 即求解

$$Cov[\widetilde{X},\widetilde{Y}]=Cov\left[ \frac{X}{\sqrt{V[X]}},\frac{Y}{\sqrt{V[Y]}} \right]=\frac{Cov[X,Y]}{\sqrt{V[X]}\sqrt{V[Y]}}$$

这一除去比例干扰的指标称为相关系数$ \rho_{XY}$. 可以验证, 对X和Y进行缩放将不会改变$ \rho_{XY}$的大小. 相关系数具有如下的特点

取值范围在-1和+1之间
相关系数绝对值越大,(X,Y)就越接近于一条直线
如果X和Y相互独立, 则相关系数为0

协方差矩阵

设有任意三个随机变量X1, X2, X3, 那么协方差矩阵的定义为

X	X1	X2	X3
X1	$Cov[X_1,X_1]$	$Cov[X_1,X_2]$	$Cov[X_1,X_3]$
X2	$Cov[X_2,X_1]$	$Cov[X_2,X_2]$	$Cov[X_2,X_3]$
X3	$Cov[X_3,X_1]$	$Cov[X_3,X_2]$	$Cov[X_3,X_3]$

如果令$X=(X_1,X_2,…,X_n)^T$, 则可以用X表示这几个随机变量构成的列向量, 此时可以得到如下的一些结论

$$
E[X] = E[(X_1,X_2,…,X_n)^T] = (E[X_1],E[X_2],…,E[X_n])^T\\
V[X] = E[(X-\mu)(X-\mu)^T]
$$

可以验证, V[X]与前面定义的协方差矩阵具有同样的形式.

对于任意取值确定的常向量a和矩阵A, 有
$$
E[a \cdot X] = a \cdot E[X] \\
E[AX] = AE[X]
$$

如果将X换成随机变量构成的矩阵, 上述关系依然成立.

对于方差, 同样可以用矩阵形式得到如下的一组性质
$$
V[a^TX]=a^TV[X]a \\
V[AX]=AV[X]A^T
$$

对于矩阵性质, 可以按照如下的方式证明:

$$
V[AX] = E[(AX-A\mu)(AX-A\mu)^T] = E[A(X-\mu)((X-\mu)^TA^T)] = E[A(X-\mu)(X-\mu)^TA^T] = AV[X]A^T
$$

多元正态分布

对于一个列向量$Z = (Z1,Z2, …, Zn)^T$, 如果其中每个分类都是服从标准正态分布的i.i.d变量, 则称Z服从n元标准正态分布.

相应的概率密度函数可以表达为

$$f_Z=g(z_1)g(z_2) \cdots g(z_n)=c exp\left(-\frac{z_1^2}{2}\right) \cdot cexp\left(-\frac{z_2^2}{2}\right)\cdots cexp\left(-\frac{z_n^2}{2}\right) = d exp\left(-\frac{1}{2} ||z||^2 \right)$$

由此可以显然的得到一个结论, 概率密度的等值面是一个圆(或者球面,超球面). 因为概率密度的表达式中只与Z的模相关,而与具体的Z取值无关.

通过简单计算可知, n元正态分布的期望向量是0向量, 协方差矩阵是单位矩阵.

参数估计

没有给出分布的具体函数形式的问题成为非参数估计. 期望值和方差不确定, 但遵从正态分布的问题称为参数估计.

在参数估计问题中, 通常将n个实际观测的数据记为$ X=(X_1,X_2,…,X_n)$, 需要估计的参数$\theta$的估计值记为$\hat{\theta}$. 由于数据X取值随机, 因此$\hat{\theta}$也是随机值. 为了强调这一点, 有时将$\hat{\theta}$成为估计量, 或记为$\hat{\theta}(X)$.

最小无偏估计

$$E[\hat{\theta}(X)] = \theta$$

贝叶斯估计

根据前面提到的贝叶斯公式, 我们有

$$ P(A|B) = \frac{P(A, B)}{P(B)} = \frac{P(B|A)P(A)}{\sum P(B|A_i)P(A_i)}$$

如果我们现在有A事件的概率分布(称为先验概率), 现在想要知道在B事件发生后A的概率变化(称为后验概率), 那么实际上就是求解$P(A|B)$.

关于贝叶斯估计在更新对违禁药物使用嫌疑的怀疑这一例子上, 可以参考文章贝叶斯统计2.

其他检验方法

交叉检验法(cross validation, CV)
赤池信息量准则(Akaike’s information criterion, AIC)
贝叶斯信息量准则(Bayesian information criterion, BIC)
最小描述长度(minimum description length, MDL)

检验理论

假设甲乙两人共进行了100场比赛, 其中甲61胜39负, 现在希望证明甲对乙的胜率大于$\frac{1}{2 }$. 此时可以建立两种假设

虚无假设$H_0$: 甲获胜的概率=$\frac{1}{2 }$
对立假设$H_1$: 甲或是的概率>$\frac{1}{2 }$

这里涉及到这样一个逻辑: 如果$H_0$成立, 则出现现在的结果的概率为p, 如果p的值非常小, 则$H_0$很有可能是错误的, 因此$H_1$更有可能正确. 我们需要支持的是$H_1$, 但我们通过证明$H_0$可能是错误的来证明$H_1$.

上面提到的$H_0$成立的概率称为p值. 我们先设定一个很小的值$\alpha$, 并且通过比较p值是否大于$\alpha$作为判断依据

p值 < $\alpha$ -> 拒绝$H_0$ (reject)
p值 >= $\alpha$ -> 无法拒接$H_0$ (accept)

由此可以产生两种术语

第一类错误(false reject): 本应为$H_0$却错误的拒绝了. 也称为弃真错误
第二类错误(false accept): $H_0$不是正确答案却错误的接受了. 也称为存伪错误

对于第一类错误, 我们做出了$H_0$不对的判断, 而对于第二类错误, 我们做出了$H_0$证据不足无法反驳的判断, 因此通常而言, 我们都希望先限制第一类错误发生的概率, 然后选择第二类错误发生概率小的方案.

最后更新： 2024年04月23日 00:19

原始链接： https://lizec.top/2019/10/05/%E5%86%8D%E8%AF%BB%E6%A6%82%E7%8E%87%E8%AE%BA/

X	X1	X2	X3
X1	\(Cov[X_1,X_1]\)	\(Cov[X_1,X_2]\)	\(Cov[X_1,X_3]\)
X2	\(Cov[X_2,X_1]\)	\(Cov[X_2,X_2]\)	\(Cov[X_2,X_3]\)
X3	\(Cov[X_3,X_1]\)	\(Cov[X_3,X_2]\)	\(Cov[X_3,X_3]\)

LiZeC的博客

通用性的代价是抽象